Volatility Skew in Equity Options Markets

What is Implied volatility?

For any given option, it represents the market's expectation of future realised volatility of the underlying equity up to the given maturity, in the proximity of the option strike.

Why does Skew exist in equity markets?

• Supply and demand - Equity market investors often BUY PUTS to safeguard their portfolios against market drawdowns and SELL CALLS to earn some income or yield on their stock holdings. Because of the regular flows in the options market, market makers and liquidity providers, such as banks, are able to demand a higher price for downside puts that they regularly sell to clients. It also means they'll be willing to pay less on upside calls, which they'll be getting from client sellers on a regular basis.
• The second reason why skew exists in equities, is empirical. When markets rise, volatility is normally quite low, and markets are calm and orderly.  However, when markets drop, the swings in price become much bigger and volatility is higher. This occurs as a result of the emotions generated when markets fall and people get frightened of losing money and panic. Panic often induces more volatility which in turn creates more panic and so on.
• Any moves down in spot trigger people to buy protection which makes implied volatility go up due to the increase in demand for options, particularly puts.

What are the causes of movements in the volatility surface?

The movements in this surface will be determined by:

• The options market's perceptions of future realised volatility across multiple time frames
• The expected tail risk in markets for large shocks in either direction
• Supply and demand of options due to large client flows

What are Dynamic Greeks?

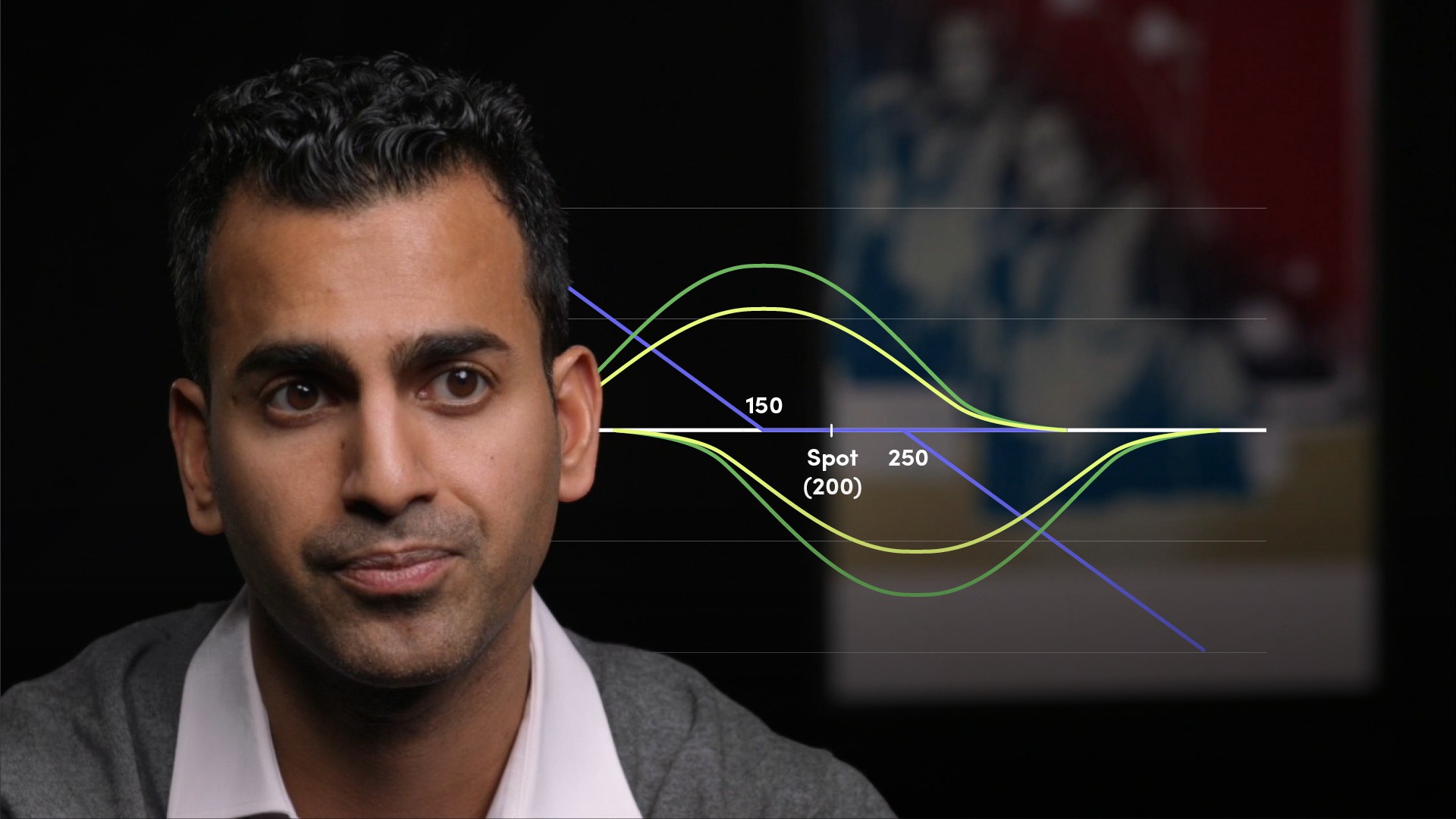
If a trader has positions in multiple options of different strikes and maturities, their Greek profiles can vary considerably.  Let's take an example of a risk reversal, where you trade a downside put and upside call in opposing directions. Let’s say both options expire in 1 month.  I sell the 90% PUT and I buy the 110% CALL.  If we plot the Gamma profile of both positions on the same graph, SHORT PUT in red and LONG CALL in blue. We will see the peak in Gamma of each individual option happens when the spot is at the respective strike. But when we sum the two Gamma profiles together to get the Green line, we will see that the overall Greek profile takes an interesting shape. When the market is at 100% of spot, the net Gamma is close to zero, as the Gamma or each options position (short put and long call) is offsetting.  However, as the spot moves either up or down, we move closer to one strike but further away from the other. Moving along the green combined profile, we see that our gamma becomes short if we move down in spot, but it becomes long if we move up in spot.  This change in Gamma or Greek profile is what we refer to as dynamic Greeks.