FX Options Case Study

How would you price a EUR put - USD call?

If we were to buy 10 million of the 3-month $1.35 strike EUR put - USD call, what would we have bought? 

It is an option on the euro dollar, so the euro is the currency that we are buying and selling, i.e. €10m. The option is a put, so it is an option to sell €10m at a strike price of $1.35.  

At expiration, if EUR-USD ends up below $1.35, we would exercise the option and receive $13.5 million in exchange for the €10 million.

Now we understand what the option is, we can value it.

Assume the 3-month forward on EUR-USD is 1.3485, and EUR-USD volatility is 7%. We can build the distribution using Lindsey’s simple option pricing model and calculate the value at expiry as shown in the diagram: 

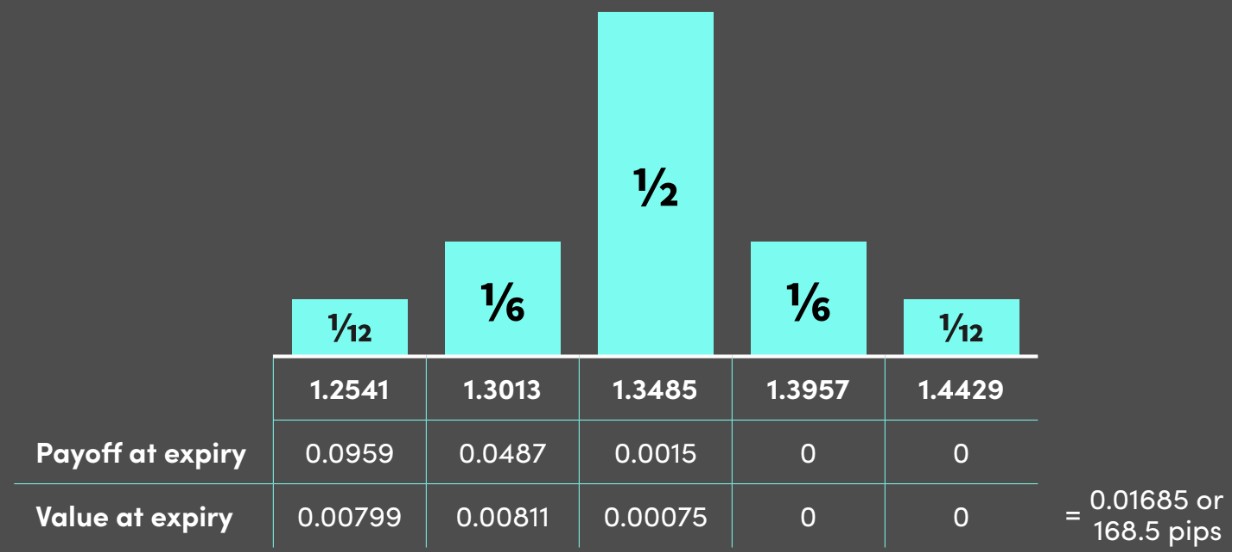
Given this is an option on EUR - USD, the prices are in dollar terms. 

How would you price a GBP call - CHF put?

This example is from interest rates were much higher. 

In July 2001, GBP/CHF was trading at 2.4603, the GBP 2-year rate was 5.64% and the 2-year CHF rate was 3.07%. The 2-year forward was 1190 pips lower at 2.3413 and volatility is at 8.4%. 

Let’s say we want to value the at-the-money options. We can calculate this using the simple model for ATMF options using the approximation Lindsey outlined in an earlier video: 

0.4 x 2.3413 x 8.4% x sqt(2) = 0.11411

Discounting this back using the Swiss rate of 3.07% gives: 

0.1111 / 1.0307^2 = 0.1047 or 1047 pips