What are Z-scores and How are they Calculated?

Abdulla Javeri
30 years: Financial markets trader
Standard normal curves and Z-scores are concepts that are often covered at school or college. Abdulla provides a refresher on the subject by outlining an example of a standard normal curve and identifying some useful excel functions to calculate a Z-score.
Standard normal curves and Z-scores are concepts that are often covered at school or college. Abdulla provides a refresher on the subject by outlining an example of a standard normal curve and identifying some useful excel functions to calculate a Z-score.
Subscribe to watch
Access this and all of the content on our platform by signing up for a 7-day free trial.

What are Z-scores and How are they Calculated?
4 mins 49 secs
Key learning objectives:
Define z-score
Learn how to calculate z-scores
Overview:
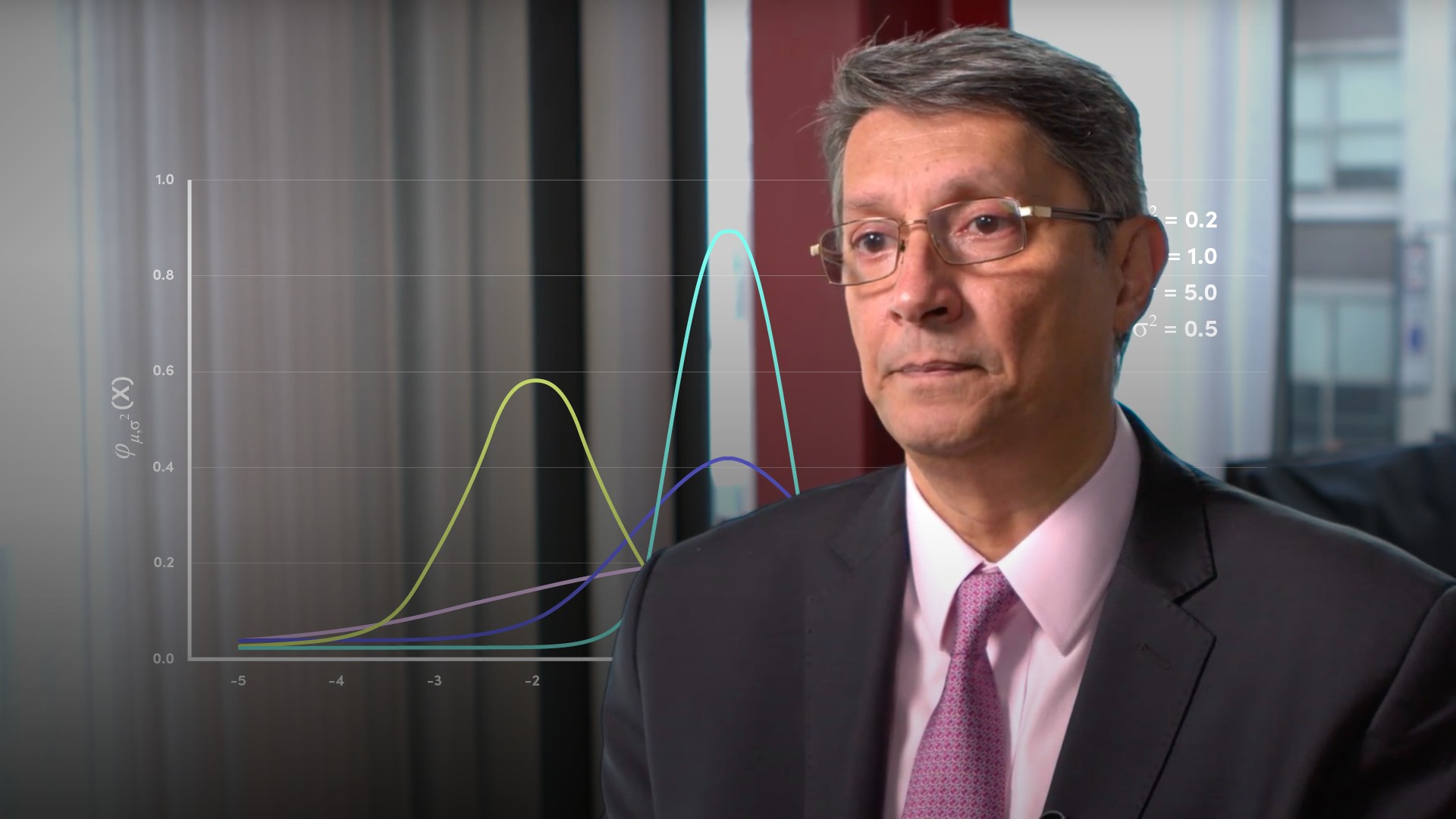
Z-scores are a crucial aspect of understanding probability distributions. The z-score can be defined as the distance from the mean as measured in standard deviations.
Subscribe to watch
Access this and all of the content on our platform by signing up for a 7-day free trial.
What are z-scores?
One thing they all have in common though is that the area of the curve that lies between two equidistant points from the mean is identical. Approximately 68% of the area under the curve lies between -1 and +1 standard deviations, and about 95.00% between -2 and +2 standard deviations.
Given that there are an infinite number of curves and they all have the same characteristics, we can represent all those curves using just one curve, the standard normal curve. In the standard normal curve the x axis scale is in standard deviations. We can look up probabilities in terms of how many standard deviations any chosen point is away from the mean. The mean is zero because the distance of the mean from the mean is zero. The distance from the mean as measured in standard deviations is the z-score.
How are z-scores represented on the curve?

Here’s a standard normal curve. As we can see, the scale is in z-scores or standard deviations. For any point x we have to determine its z-score. It’s simply x minus the mean divided by the standard deviation. From there we can look up the area of the curve to the left of that point.
How do we calculate z-scores?
Example 1 - Assume the following:
- Mean = 500
- Standard deviation = 40
- X = 520
z= (520-500)/40 = 0.5
Example 2 - Assume the following:
- Mean = 500
- Standard deviation = 40
- X = 480
z= (480-500)/40 = -0.5
Subscribe to watch
Access this and all of the content on our platform by signing up for a 7-day free trial.

Abdulla Javeri
There are no available Videos from "Abdulla Javeri"



























